탐색(Search)
- 탐색(Search) : 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정
Ex. DFS, BFS, Graph, Tree..
DFS와 BFS 알고리즘을 제대로 이해하려면 기본적인 자료구조인 스택, 큐에 대한 정리가 요구되므로 간단히 정리한다.
스택(Stack)과 큐(Queue)는 자료 구조(Data Structure)의 일종
+) 자료구조 : 데이터를 표현하고 관리, 처리하기 위한 구조
주요 함수 및 고려해야 할 점
- 삽입(Push) : 데이터 삽입
- 삭제(Pop) : 데이터 삭제
- 오버플로(Overflow) : 자료구조가 수용 가능한 데이터의 크기를 이미 가득 찬 상태, 삽입 연산을 수행할 때 발생
- 언더플로(Underflow) : 자료구조에 데이터가 전혀 들어있지 않은 상태, 삭제 연산을 수행할 때 발생
스택(Stack)
Stack(스택) : 박스 쌓기
선입후출(First In Last Out, FILO)구조 또는 후입선출(Last In First Out, LIFO) 구조


Ex) 초기 단계 - 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
stack = []
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
stack.append(5)
stack.append(2)
stack.append(3)
stack.append(7)
stack.pop()
stack.append(1)
stack.append(4)
stack.pop()
print(stack) # 최하단 원소부터 출력
print(stack[::-1]) # 최상단 원소부터 출력

파이썬에서는 스택을 사용할 때 별도의 라이브러리가 필요없다. 기본 리스트에서 append와 pop메서드를 사용하면 스택 자료구조와 동일하게 동작한다. append()는 리스트의 가장 뒤쪽에 데이터를 삽입하고, pop()메서드는 리스트의 가장 뒤쪽에서 데이터를 꺼낸다.
큐(Queue)
Queue(큐) : 일종의 대기줄로 입구와 출구가 모두 뚫려있는 터널
선입선출(FIFO, First in First out) 구조


Ex) 초기 단계 - 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
from collections import deque
# 큐(Queue) 구현을 위해 deque 라이브러리 사용
queue = deque()
# 삽입(5) - 삽입(2) - 삽입(3) - 삽입(7) - 삭제() - 삽입(1) - 삽입(4) - 삭제()
queue.append(5)
queue.append(2)
queue.append(3)
queue.append(7)
queue.popleft()
queue.append(1)
queue.append(4)
queue.popleft()
print(queue) # 먼저 들어온 순서대로 출력
queue.reverse() # 다음 출력을 위해 역순으로 바꾸기
print(queue) # 나중에 들어온 원소부터 출력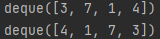
파이썬으로 큐를 구현할 때는 collections module에서 제공하는 deque 자료구조를 활용한다. deque는 스택과 큐의 장점을 모두 채택한 것으로 데이터를 넣고 빼는 속도가 리스트 자료형에 비해 효율적이고, queue 라이브러리를 쓰는 것보다 더 간단한다. 더불어 대부분 코테에서는 collections 모듈과 같은 기본 라이브러리 사용을 허용하기때문에 안심해도 좋다.
재귀함수(Recursive Function)
재귀함수는 아래 예제 처럼 자기 자신을 다시 호출하는 함수를 의미한다.
def recursive_func():
print('재귀함수 호출')
recursive_func()
recursive_func()이 코드를 수행하면 "재귀함수 호출"이라는 문자열을 무수히 출력하다가 아래와 같은 오류를 출력하고 멈출 것이다.

이 오류메시지는 재귀의 최대 깊이를 초과했다는 내용이다. (일반적인 파이썬 인터프리터는 호출 횟수 제한이 있는데 그걸 벗어났다는 의미)
재귀 함수의 종료 조건
재귀 함수를 문제 풀이에서 사용할 때는 재귀함수가 언제 끝날지, 종료 조건을 꼭 명시해야 한다. 자칫 종료 조건을 명시하지 않으면 아까와 같이 함수가 무한 호출될 수 있다. 아래 예제는 if문으로 종료 조건을 명시한 예제이다.
def recursive_function(i):
# 100번째 출력했을 때 종료되도록 종료 조건 명시
if i == 100:
return
print(i, '번째 재귀 함수에서', i + 1, '번째 재귀 함수를 호출합니다.')
recursive_function(i + 1)
print(i, '번째 재귀 함수를 종료합니다.')
recursive_function(1)
재귀함수로 구현한 팩토리얼 vs 반복적으로 구현한 팩토리얼
# 반복적으로 구현한 n!
def factorial_iterative(n):
result = 1
# 1부터 n까지의 수를 차례대로 곱하기
for i in range(1, n + 1):
result *= i
return result
# 재귀적으로 구현한 n!
def factorial_recursive(n):
if n <= 1: # n이 1 이하인 경우 1을 반환
return 1
# n! = n * (n - 1)!를 그대로 코드로 작성하기
return n * factorial_recursive(n - 1)
# 각각의 방식으로 구현한 n! 출력(n = 5)
print('반복적으로 구현:', factorial_iterative(5))
print('재귀적으로 구현:', factorial_recursive(5))
반복과 재귀함수의 차이점을 비교해보면 재귀함수가 더 간결한 것을 확인할 수 있다. 이는 재귀형식이 수학의 점화식을 그대로 소스코드로 옮겼기 때문이다.

탐색 알고리즘 DFS/BFS
- Graph(그래프) : 노드(Node=Vertex)와 간선(Edge)로 표현되며, 그래프 탐색은 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 말한다. 두 노드가 간선으로 연결되어 있다면 두 노드는 인접하다(Adjacent)라고 표현한다.

- 그래프의 표현 방식
- 인접행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현하는 방식(연결되어 있지 않으면 무한)
- 인접리스트(Adjacency List): 리스트로 그래프의 연결 관계를 표현하는 방식
메모리 측면에서 보면 인접행렬 방식이 모든 관계를 저장하기 때문에 노드 개수가 많으면 메모리가 불필요하게 낭비
반면, 인접 리스트 방식은 연결된 정보만을 저장하기에 메모리를 효율적으로 사용 But 인접 행렬에 비해 두 노드가 연결됐는지 여부에 대한 정보를 얻는 속도가 느림.(일일히 하나씩 확인해야 되서)


#### 인접 행렬 방식 예제 ####
INF = 999999999 # 무한의 비용 선언
# 2차원 리스트를 이용해 인접 행렬 표현
graph = [
[0, 7, 5],
[7, 0, INF],
[5, INF, 0]
]
print(graph)
#### 인접 리스트 방식 예제 ####
# 행(Row)이 3개인 2차원 리스트로 인접 리스트 표현
graph = [[] for _ in range(3)]
# 노드 0에 연결된 노드 정보 저장(노드, 거리)
graph[0].append((1, 7))
graph[0].append((2, 5))
# 노드 1에 연결된 노드 정보 저장(노드, 거리)
graph[1].append((0, 7))
# 노드 2에 연결된 노드 정보 저장(노드, 거리)
graph[2].append((0, 5))
print(graph)
- DFS(Depth-First Search) : 깊이 우선 탐색
= 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘
= 특정한 경로로 탐색하다가 특정한 상황에서 최대한 깊숙이 들어가서 노드를 방문한 후, 다시 돌아가 다른 경로로 탐색하는 알고리즘
1) 탐색 시작 노드를 스택에 삽입, 방문처리 함
2) 스택의 최상단 노드에 방문하지 않은 인접노드가 있을 시, 그 인접 노드를 스택에 넣고 방문 처리/ 방문하지 않은 인접노드가 없으면 스택에서 최상단 노드를 꺼냄
3) 2번의 과정을 더 이상 수행할 수 없을 때 까지 반복
'Coding TEST' 카테고리의 다른 글
| [코딩 테스트 with 파이썬] Chapter 04. Implementation (2) | 2021.07.26 |
|---|---|
| [Python] itertools 모듈 / 내장 함수(zip, map ..) (0) | 2021.06.01 |
| [Codility_16. Greedy Algorithm] MaxNonoverlappingSegments (3) | 2021.05.21 |
| [코딩 테스트 with 파이썬] 0. Introduction (0) | 2021.05.20 |
| [코딩 테스트 with 파이썬] Chapter 03. Greedy (0) | 2021.05.18 |
