※ 본 게시물은 Pytorch 기초 강의 9. DQN 포스팅의 이해를 위해 작성한 부가 포스팅입니다.
강화학습(Reinforcement Learning)
강화학습 : 보상(reward), 처벌(penalty)를 미리 설계하고 스스로 환경을 경험하며 학습(from.포스팅)
= 환경과 상호작용하여 좋은 점수를 얻는 방향으로 성장
= 사람은 목표를 설정해주고 당근과 채찍을 이용해 성장시키는 코치의 역할
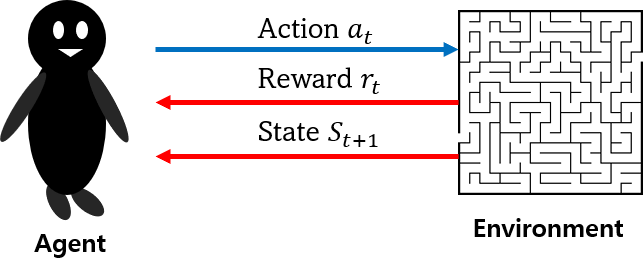
강화학습의 구성요소
1. 에이전트(agent) : 인공지능 플레이어
2. 환경(environment) : 에이전트가 솔루션을 찾기 위한 무대
3. 행동(action) : 에이전트가 환경 안에서 시행하는 상호작용
4. 보상(reward) : 에이전트의 행동에 따른 점수 혹은 결과
강화학습의 사례
- 알파고
- 로봇
- 비디오 게임
...


MDP(Markov Decision Process)
강화학습은 MDP로 표현된 문제를 푸는 알고리즘의 집합
MDP : 순차적인 행동 결정과정을 수학적으로 표현한 것
강화학습의 구성요소
MDP = <S, A, P, R, γ>
- 상태(State $S = {s_{1}, s_{2}, ..., s_{t}}$)
: 에이전트가 현재 인신하고 있는 자신의 위치(=환경의 전체 상태)
- 행동(Action $A={a_{1}, a_{2}, ..., a_{t}}$)
: 에이전트가 특정 state에서 취하는 행동
- 상태 변환 확률(State transition probability matrix, $P[S_{t+1}=s'|S_{t}=s, A_{t}=a]$)
: 에이전트가 어떤 행동을 취했을 때 현재 state($s_{t}$)에서 다음 state로 변환될 확률($s_{t+1}$)
- 보상함수(Reward $R = E[R_{t+1}|S_{t}=s, A_{t}=a]$)
: 에이전트가 행동을 수행했을 때 환경으로부터 받는 보상(=상태, 행동 쌍이 얼마나 유의미한가 외부에서 채점)
- 감가율(Discount Factor, γ∈[0, 1])
: 미래의 보상(reward)를 얼마만큼 고려할 것인가(=시간에 따라 가치를 판단하는 척도)
--> (ex. 오래된 가치는 그만큼 가치가 떨어지게 평가해야함)
- 정책(Policy)
: 에이전트의 행동 정책
(1) Deterministic Policy : 주어진 state에 대해서 한 가지 정해진 Action이 존재함. $π(a|s)=a$
(2) Stochastic Policy : 주어진 state에 대해서 Action들의 확률 분포에 따라 결정. $π(a|s) = P[A_{t} = a|S_{t} = s]$
- Return ($G_{t}=R_{t+1}+γR_{t+2}+γ^2R_{t+3}+...$)
: 현재 state로부터 미래의 보상을 고려하여 예측한 보상의 합
State과 action이 나중에 어느 정도의 reward를 돌려줄지에 대한 예측 함수
(=해당 state과 action을 취했을 때 이후에 받을 모든 reward 들의 가중합)
- Value
: 해당 상태/행동이 얼마나 가치있는가
(1) State-Value Function : 현재 상태 s에서 앞으로 받을 리턴에 대한 기댓값
$V_{π}(s)=E_{π}[G_{t}|S_{t}=s]$
(2) Action-Value Function : 현재 상태 s에서 어떤 행동 a를 했을 때 받을 리턴(return)에 대한 기대값
$q_{π}(s,a)=E_{π}[G_{t}|S_{t}=s, A_{t}=a]$
[에이전트의 행동 선택 전략]
1) 매 순간($t$ 타임마다) 행동을 선택하면서 얻는 단기적인 보상(immediately reward)으로 동작
=> 단기적인 보상만으로는 충분한 최적의 정책(policy)를 얻기 힘듦.
ex) - sparse reward : 바둑과 같은 장기전의 게임에서는 승패가 늦게 알려짐=="reward를 적게 받는 경우"
- delayed reward : 바둑에서 한 수 둘 때마다(==매 순간 행동을 선택할 때마다) reward를 줄 수 없는 경우.
2) 현재, 미래의 보상(장기적인 보상)을 보고 행동을 결정하는 동작
- 단순합($R_{1}+R_{2}+R_{3}+...+R_{T}$) : 앞으로 받을 모든 합을 더한다.
한계 1) 현재 받은 reward나 미래에 받는 reward를 동일하게 취급한다.
한계 2) 단순 보상의 합으로는 판단내리기 쉽지 않다.
- Return ($G_{t}=R_{t+1}+γR_{t+2}+γ^2R_{t+3}+...$)
: 현재 state로부터 미래의 보상을 고려하여(감가율을 적용한) 예측한 보상의 합
State과 action이 나중에 어느 정도의 reward를 돌려줄지에 대한 예측 함수(=해당 state과 action을 취했을 때 이후에 받을 모든 reward 들의 가중합)
에피소드가 다 끝난 후에 그동안 받았던 보상을 정산
한계 1) 에피소드가 다 끝난 다음에야 해당 return값을 받을 수 있음.
- Value : 해당 상태/행동이 얼마나 가치있는가
(1) State-Value Function : 현재 상태 s에서 앞으로 받을 리턴에 대한 기댓값
상태 s로만 정해지는 값으로 가능한 반환값들의 평균을 구해서 진행
$V_{π}(s)=E_{π}[G_{t}|S_{t}=s]$
$== V_{π}(s)=E_{π}[R_{t+1}+γv_{π}(S_{t+1})|S_{t}=s]$== 벨만 방정식
(2) Action-Value Function : 현재 상태 s에서 어떤 행동 a를 했을 때 받을 리턴(return)에 대한 기대값
: 다 직접 경험해보지 않고 기댓값에 의해서 보상을 예측, 정책에 영향을 많이 받음, 상태 s로만 정해지는 값으로 가능한 반환값들의 평균
$q_{π}(s,a)=E_{π}[G_{t}|S_{t}=s, A_{t}=a]$
$== q_{π}(s,a)=E_{π}[R_{t+1}+γq_{π}(S_{t+1}, A_{t+1})|S_{t}=s, A_{t}=a]$ == Q함수
'머신러닝 > 머신러닝 기초 개념' 카테고리의 다른 글
| [머신러닝 통계학] 3.통계적 추론 (0) | 2021.07.28 |
|---|---|
| [머신러닝 통계학] 2.기술통계 (0) | 2021.07.28 |
| [머신러닝 통계학] 1.소개 (0) | 2021.07.27 |
| Numpy Seed 설정 (np.random.seed(0), np.random.seed(42)) (0) | 2021.07.02 |
| Domain Adaptation(Domain-Adversarial Training of Neural Networks) (0) | 2021.06.05 |
