728x90
반응형
머신러닝 통계학 핵심 개념
- 가설 검정
: 표본에 대한 통계적 테스트를 수행해, 전체 모집단에 대한 추론을 생성하는 과정, 귀무가설(H0), 대립 가설(연구가설, H1)을 통해 가정이 통계적으로 의미가 있는지 검정
: 모델링에서 각 독립 변수에 대해 0.05(5% 미만)보다 작은 p-value는 유의미하다고 간주.
- 가설 검정의 단계
: [귀무가설 정의] → [표본 추출] → [검정 통계량에 따른 귀무가설의 통계적 유의성(p-value) 확인] → [검정 통계량에 따라 귀무가설 채택(p-value 0.05 이상) 또는 기각(p-value 0.05 미만)]
- p-value : 귀무가설이 옳다는 전제 하에 표본에서 실제로 관측된 통계값과 같거나 더 극단적인 통계값이 관측될 확률
ex) 한 빵집에서 생산되는 식빵의 무게가 최소 200g이라 주장할 경우, 표본 20개를 추출해 구한 평균 무게가 196g이고, 표준 편차는 5.3g이었다면, 유의수준 5%(0.05)로 위의 주장을 기각할 수 있을까?
--> 귀무가설 : 모든 식빵의 무게는 200g 이상이다.
표본 : 평균() =196 / 표준 편차 = 5.3 / 표본의 크기 = 20개

import numpy as np
from scipy import stats
x_bar, mu, s, n = 196, 200, 5.3, 20
t_sample = (x_bar - mu) / (s/np.sqrt(float(n)))
print('검정 통계량 : ', np.round(t_sample, 2))
alpha = 0.05
t_alpha = stats.t.ppf(alpha, n-1)
print('t-table로부터의 임계값 : ', np.round(t_alpha, 3))
p_val = stats.t.sf(np.abs(t_sample), n-1)
print('t-table의 아래쪽 꼬리 p값', np.round(p_val, 4))
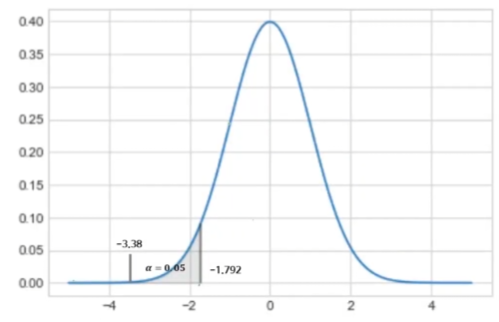

p-value가 0.05보다 작기때문에 귀무가설 기각
= 우리 식빵은 200g 이상이다! ==> 기각/ 통계적으로 유의하지 않다.
- 정규분포
: 중심극한정리에 따르면 평균이 $\mu$이고, 분산이 $\sigma^{2}$(표준편차가 $\sigma$)인 모집단으로부터 가능한 모든 $n$개의 조합을 표본으로 추출하면 표본의 평균은 정규 분포에 접근함.

ex) 시험 점수가 정규분포를 따른다고 가정할 경우, 평균 점수가 56점이고, 표준편차가 13.6인 경우 75점 이상을 받은 학생들은 몇%인가
정규분포를 따르기 때문에 표준정규분포로 바꿔 계산 --> 평균 0 , 분산 1 $N(0,1)$
표준점수(z-score)가 == 75-56 = 13.6(표준점수)
import numpy as np
from scipy import stats
x_bar, mu, s = 75, 56, 13.6
z = (x_bar - mu)/s
print('z-score',np.round(z,2))
p_val = 1-stats.norm.cdf(z)#누적확률분포함수
print('학생이 {}점 이상 받을 확률:{}%'.format(x_bar, np.round(p_val*100,2)))

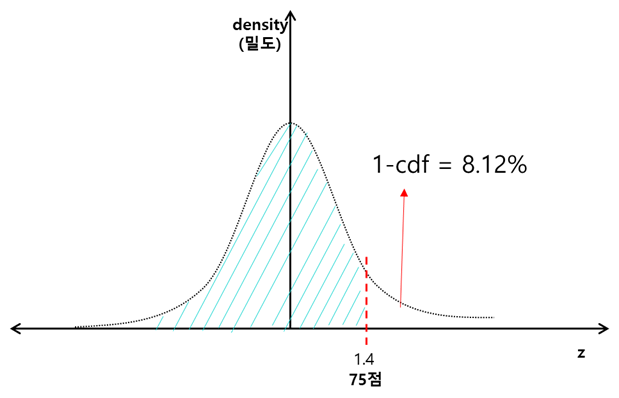
- 카이제곱 독립성 검정
: 범주형 데이터의 통계 분석에 가장 보편적으로 사용되는 검정, 2개의 범주형 변수 사이에 통계적 상관성이 존재하는지 여부를 판단.

ex) 흡연이 운동에 영향을 미칠까
import numpy as np
import pandas as pd
from scipy import stats
np.random.seed(0)
# 데이터 생성 단계
smoke=["안함","가끔", "매일", "심함"]
exercise = ["안함","가끔", "매일"]
data = {"smoke":np.random.choice(smoke, size = 500),"exercise":np.random.choice(exercise,size = 500)}
df = pd.DataFrame(data, columns=["smoke","exercise"])
df.head()
# 분할표 생성단계
xtab = pd.crosstab(df.smoke, df.exercise)
print(xtab)
contg = stats.chi2_contingency(observed=xtab)
p_val=np.round(contg[1],3)
print('p-value : ',p_val)
-ANOVA(Analysis of Variance) 분산 분석
: 모집단이 셋 이상인 경우, 이들의 평균이 서로 동일한지 테스트함
- 귀무가설 : 모든 모집단의 평균에 차이가 없다.
- 대립가설 : 적어도 하나의 모집단의 평균에 차이가 있다.
+) t-검정은 두 집단의 평균 차이/ ANOVA는 셋 이상의 평균 차이 검정
ex) 10명의 환자를 대상으로 A,B,C 세가지의 수면제 약효(수면 시간)을 테스트할 경우, 유의수준 0.05에 대해서 A,B,C 수면제의 평균 수면 시간은 동일한가?
import numpy as np
import pandas as pd
from scipy import stats
np.random.seed(0)
data = (np.random.rand(30).round(2)*10).reshape(-1,3)
df = pd.DataFrame(data=data, columns=["A", "B", "C"])
print(df)
one_way_anova = stats.f_oneway(df.A, df.B, df.C)# 일원분산분석
print('통계량 : {}, p-value : {}'.format(np.round(one_way_anova[0], 2), np.round(one_way_anova[1],3)))
==> p-value가 0.173으로 귀무가설(세개의 수면제 약효 평균이 동일하다) 채택
본 포스팅은 하단 영상을 보고 정리한 내용입니다.
728x90
반응형
'머신러닝 > 머신러닝 기초 개념' 카테고리의 다른 글
| 머신러닝 관련용어 (A to Z) (0) | 2021.09.01 |
|---|---|
| [머신러닝 통계학] 2.기술통계 (0) | 2021.07.28 |
| [머신러닝 통계학] 1.소개 (0) | 2021.07.27 |
| Numpy Seed 설정 (np.random.seed(0), np.random.seed(42)) (0) | 2021.07.02 |
| 강화학습(Reinforcement Learning) (0) | 2021.06.20 |
